John and Alicia Nash, 1928,1933–2015

Post by  KWRegan published to RJ Lipton's blog, "Gödel's lost letter and P=NP", on 25/05/2015

Our condolences 

Awesome Stories source

John Nash and his wife Alicia were killed in a taxi accident on the New Jersey Turnpike Saturday afternoon. They were on their way back from Norway where he and Louis Nirenberg had just accepted the 2015 Abel Prize. Besides meeting the king of Norway, Nash had also expressed a desire to meet world chess champion Magnus Carlsen during remarks at Princeton’s celebration of his Abel Prize in March, and that was also granted this past week.

Today Dick and I join many expressing shock and offering condolences.

The time spans for the Nashes are really 1957–1963, 1970–2000, and 2001–2015. They were married in 1957, two years before the onset of John’s schizophrenia. Their divorce in 1963 came amid a nine-year series of hospitalizations that began in 1961. After his discharge in 1970, she felt he would be better off boarding in a room of the house she’d moved to in Princeton Junction than in an institution or on his own. This stable arrangement with a balance of connection and detachment is credited with helping him regain normalcy as his paranoia abated in the late 1980s. Lucidity in the 1990s cleared the way for his Nobel Prize and re-integration into Princeton’s mathematics community and with his family. He and Alicia re-married in 2001 and both contributed to a positive equilibrium.

I first saw the news early Sunday morning on BBC.com while going to check the England-New Zealand Test cricket score. It was the lead story on CNN.com for part of this afternoon. Many stories continue to emerge, among which we mention the NY Times (longer obit), Princeton, a local Princeton site, and appreciations by Peter Woit of Columbia and by Frederic Friedel of ChessBase GMBH. The last two include short personal recollections.

Abel Prize source; see also our earlier post.

Alicia’s All

Alicia’s life was one of boldness and courage from the day she emigrated with her family from El Salvador in 1944. Her father had followed her uncle fearing backlash against their aristocratic family from a popular insurrection. Hearing about the nuclear bomb on the radio inspired her to become an atomic physicist, and she worked hard to become one of only seventeen women in MIT’s class of 1955.

Nash was then in MIT’s math department, and she met Nash on a warm day in the first lecture of his advanced calculus course. She defiantly re-opened windows Nash had closed to shut out noise and left the class with an indelible crush. They started dating after she earned her physics degree. Her attachment to him survived the literal sudden emergence of his previous female partner and their child, and the revelation to some unknown degree of previous male partners. They married in early 1957 and shortly began raising a family.

The rapid phase of Nash’s descent in early 1959 was “like a tornado.” One must marvel at how she coped in the 1960s with his condition, raising their son, and finding computer-related work near Cambridge and later Princeton. She even brought a sex-and-job discrimination lawsuit against Boeing that was settled in a helpful manner in 1973, before she found a permanent computer programming position with New Jersey Transit. She then had to deal with schizophrenia in their son John, whom I briefly got to know for several days in 1980 when came around to Princeton’s Quadrangle Club.

In recent years she advocated for support of community mental health programs that enable patients to live outside hospitals. She met with New Jersey state officials during budget negotiations in 2009. Our hearts go out most to their son.

Hex and Complexity

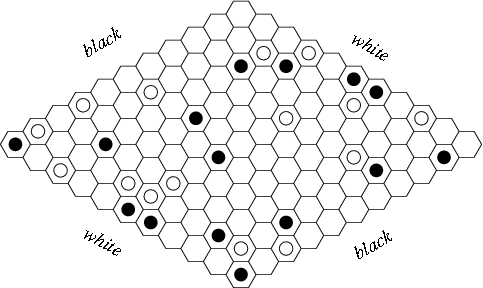
The game of Hex is played on an  rhombus of hexagons, or as Nash originally conceived it, on an  checkerboard in which squares count as adjacent also on the SW-NE diagonal but not SE-NW. White and Black alternate placing stones of their color, with White trying to form a path connecting the north and south borders, Black east-west. The corner squares count as border for either player. The game cannot end in a draw, and this fact is highly non-trivial: as shown neatly in these notes it is equivalent Brouwer’s Fixed-Point Theorem, which was later instrumental to Nash’s great work on two-player non-zero-sum games.

Wolfram MathWorld source

Hex was originally invented in 1942 by the Danish polymath Piet Hein. Nash conceived it independently from an angle that leaps out at us from this account by his fellow Princeton graduate student David Gale, as quoted in Sylvia Nasar’s biography A Beautiful Mind. Nash hailed Gale in the Princeton Graduate College quadrangle, saying:

“Gale! I have an example of a game with perfect information. There’s no luck, just pure strategy. I can prove that the first player always wins, but I have no idea what his strategy will be. If the first player loses at this game, it’s because he’s made a mistake, but nobody knows what the perfect strategy is.”

For board sizes above 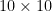, Nash’s words are still true, even with the computing might and sophisticated algorithms exerted in this 2013 paper by Jakub Pawlewicz and Ryan Hayward. The nub was proved in 1976 by Shimon Even and Bob Tarjan: deciding who stands to win a given Hex position on an  board is -complete.

We believe that Nash, plausibly earlier than Kurt Gödel, already concretely felt the contours of complexity theory for practical problems. Here it was blended with fascination at the power of a quick non-constructive argument to convey knowledge that is hard to obtain programmatically:

• The game cannot end in a draw.
• Hence either the first or second player must have a winning strategy.
• An extra move at Hex, unlike chess or checkers, can never be harmful.
• Hence if the second player had a winning strategy, the first player could commandeer it by making an arbitrary first move and then following it.
• Therefore the first player must have a winning strategy.

The depth of Nash’s thoughts about complexity was revealed in early 2012 when a handwritten letter(typed version) he wrote in 1955 to the National Security Agency was declassified. He proposed a cryptosystem with  possible keys and continued:

Now my general conjecture is as follows: For almost all sufficiently complex types of enciphering, especially where the instructions given by different portions of the key interact complexly with each other in the determination of their ultimate effects on the enciphering, the mean key computation length increases exponentially with the length of the key, or in other words, with the information content of the key.

The significance of this general conjecture, assuming its truth, is easy to see. It means that it is quite feasible to design ciphers that are effectively unbreakable. As ciphers become more sophisticated the game of cipher breaking by skilled teams, etc., should become a thing of the past.

The nature of this conjecture is such that I cannot prove it, even for a special type of ciphers. Nor do I expect it to be proven. But this does not destroy its significance. The probability of the truth of the conjecture can be guessed at on the basis of experience with enciphering and deciphering.

If qualified opinions incline to believe in the exponential conjecture, then I think we (the U.S.) cannot afford not to make use of it.

The only words here that may not be amazingly prescient—including a rimshot on the distinction between string length and information complexity—are the idea that complexity makes concrete efforts at breaking “a thing of the past.” Even for Hex, the -completeness result might not prevent the existence of a succinctly described and efficient first-player strategy. Such a strategy might avoid the kind of positions used for the hardness proof. We are reminded in crypto by a just-released paper andwebsite on the new Logjam attack on Diffie-Hellman key exchange. This is excellently covered by Scott Aaronson here, and has echoes of faults with RSA implementations that likewise fail to diversifythe prime numbers used.

Open Problems

Is there a succinct description of an efficient strategy for winning at  Hex?

Our condolences again to the family and friends of the Nashes.